Arts & Sciences, models & illustrations, Buddhas within mandalas
[ by Charles Cameron — on the illustration, visualization and modeling of supposed reality — note: I am no scientist, no artist, in fact an aphantasic ]
.
A telling caption to an image in New Scientist gave rather more of the game away than was maybe intended.
The image:

The caption:
We have no pictures of the real thing, so enjoy this one instead. Oliver Burston/Alamy
**
It’s a nice image, and could be used to represent Lise Meitner‘s discovery of nuclear fission, or some new feature of Kepler’s Supernova, or even, Lord knows, to sell collectible gold coin or diamonds.. And it brings up in acute form an issue I’ve long had with science — in the context of education and the last century’s growing indifference to the arts and humanities.
How much of what passes for science in the pop science press is in fact art, and specifically photography? And as a sub-question, how much of the impact a particular piece of scientific work receives is dependent on the various qualities of the illustrations used to accompany and promote it — which all too often fit the description in the caption above:
We have no pictures of the real thing, so enjoy this one instead.
Or alternatively, shooting for something a little more frank, but not too terribly impolite:
We have no pictures of the real thing, so enjoy this bullshit instead.
**
We hardly ever have a picture of the real thing — which occurs at nano-scale, or outside the visible spectrum, or —
Well, some while back, we discussed (ignorantly, rest assured, De Docta Ignorantia, qv) a mathematical object of interest to physicists known as The Amplituhedron:

The Amplituhedron can alternatively be illustrated thus:

There’s a donut for anyone who can imagine what can possibly merit both illustrations!
**
On our way to an understanding of the Amplituhedron, we pass by diagrams such as this:
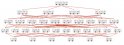
— immediately followed by these words:
Although it is hard to draw the complete four-dimensional polytope, its four three-dimensional faces each define square-pyramidal regions of G(2, 4)
— as, for instance, this:
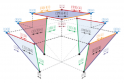
**
Oh, c’mon, it’s not that hard, just visualize it!
Tibetan monks can visualize things like this 3-D palace replete with Vases, Wish-granting Trees, Bodhisattvas, Tathagatas and Shaktis, all surrounding the deity Kalachakra and his Consort, Vishvamata —

And the vajrayanist Tibetan practitioners, yes, manage this just by PhD and postdoc level visualization practice, with diagrammatic assists like this:
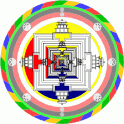
— and a blueprint like this:

— always bearing in mind that, eh, “Kalachakra is a black skinned, four-faced god with twelve arms and twenty-four hands, in passionate embrace with his consort”:
Page 1 of 2 | Next page