GBG: another form of associative linkage
[ by Charles Cameron — a meander to ponder, wonder, wander, a maze to amaze, or as CS Peirce might say, a muse to amuse, an amuse-bouche ]
.
Here’s a quick, long run-down of my HipBone games, where they came from, and where they’ll be going if book and online game plans come together.
My various HipBone and related games are intended as playable variants on Hermann Hesse‘s great Glass Bead Game (GBG for short).
You remember this?
As I said before:
I don’t know how Theodor von Kármán came by his Vortex Street, and I’ve spent a decade in Pasadena wandering its streets and even picked up his four volume works — signed — at a CalTech book sale — but if he had the Van Gogh painting in the back of his mind, there’s the beginning, the seed of an awesome leap.
And you might say van Gogh made a mighty leap, pre-intuiting the von Kármán pattern in the night sky..
This DoubleQuote is my favorite move in the game that has obsessed me for the last thirty or so years, the Glass Bead Game as described in Hermann Hesse in his Nobel-winning novel of the same name.
Linking arts and sciences as it does, I see it as a move at the nave roof-apex of what Hesse describes as the “hundred-gated cathedral of mind”.
The essence of a move in Hesse‘s game is associative linkage.
**
I’m using this post as something of a primer on my game thinking, before proposing a recent instance of a type of associative leap / example of a game move.
**
There are many fairly basic types of associative linkage that provide the connextive tissue between the items in an ontology:
this is the same as that this causes that this is the opposite of that this symbolices that this is above that this is inside that this is the parent of that this follows that this governs that this proves that
**
Getting more complex and multi-layered, John Robb once posted:
Some philosophical thinking:
Human knowledge, at an elemental level, can be described as a “transformation” of data. Complex ideas are built using layers of “transformations” with each layer feeding into the next (think pyramid) We teach these transformations at home and at school to our children. We communicate by sharing transformations. Questions We Need to Answer in the Age of Cognitive Machines:
How many transformations would it take to model all human knowledge? How deep (how many layers of transformation is human knowledge) is human knowledge? Both on average or at its deepest point? How broad is human knowledge (non-dependent transformations)? How fast is the number of transformations increasing and how fast is it propagating across the human network?
**
From a process orientation, it’s pretty clear that the fundamental way in which most associative leaps occur to human minds takes the form:
this reminds me of that
— and that holds true even of conspicuous creative leaps not just out of the box but into the unknown — as when Yutaka Taniyama proposed his hypothesis that there exists a correspondence between elliptic curves and modular forms in 1955. Andrew Wiles eventually proved the linkage in what is now known as the Modularity theorem, as the key part of his proof of Fermat’s Last Theorem in 1993 [don’t ask me to explain, I’m not a mathematician]
**
Creative leaps are in general the basis of much “opening of fields” both in the arts and sciences, as described by Arthur Koestler in his Act of Creation:
and elaborated by Douglas Hofstadter in eg his Fluid Concepts and Creative Analogies and Surfaces and Essences: Analogy as the Fuel and Fire of Thinking, and at a depth of penetration equivalent to Robb’s questions above, by Fauconnier and Turner in The Way We Think: Conceptual Blending And The Mind’s Hidden Complexities..
**
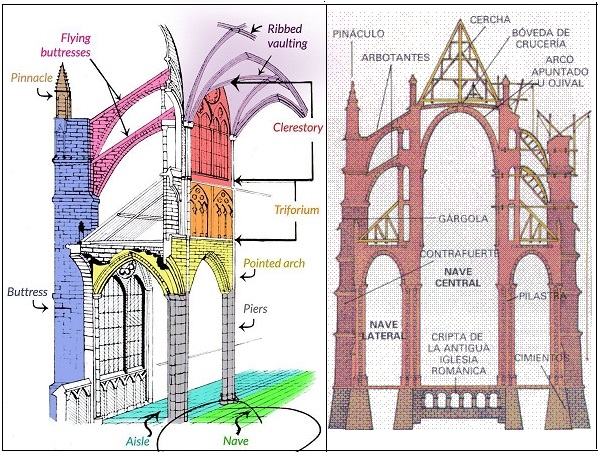
Level on level, the structure of a gothic cathedral is arch building on arch (forgive my Spanish):
Erwin Panofky‘s masterwork, Gothic Architecture and Scholasticism, argues for a common mental structure explaining the simultaneous occurrence of Gothic cathedral architecture and the scholastic argumentation characteristic of Peter Abelard and Thomas Aquinas..
**
The music of Hesse’s cathedral?
All the insights, noble thoughts, and works of art that the human race has produced in its creative eras, all that subsequent periods of scholarly study have reduced to concepts and converted into intellectual values the Glass Bead Game player plays like the organist on an organ. And this organ has attained an almost unimaginable perfection; its manuals and pedals range over the entire intellectual cosmos; its stops are almost beyond number.
And the game’s ultimate destination – besides the creation of an overarching synthesis uniting sciences and arts, great leaps of discovery and profound flights of imagination?
Every transition from major to minor in a sonata, every transformation of a myth or a religious cult, every classical or artistic formulation was, I realized in that flashing moment, if seen with a truly meditative mind, nothing but a direct route into the interior of the cosmic mystery, where in the alternation between inhaling and exhaling, between heaven and earth, between Yin and Yang, holiness is forever being created.
In the coincidence of opposites — the buttressed left side of the cathedral’s gothic arch leaning into, against and with the buttressed right side, culminating in the high vaulting that characterizes the nave — transcendence of the physical in the spiritual..
**
An aside:
Okay, very quickly, one associative link that jumped out at one poster recently after the Democratic response to Trump’s resolute desk address was the similarity between Schumer and Pelosi‘s stilted appearance, standing shoulder to shoulder at a single podium [left], and — returning to our theme of gothic as in a fugue — the celebrated painting titled American Gothic [composite, right] —
That’s a “haha!” (comedic, laughter) rather than an “aha!” (creative, excitement) or “aah!” (tragedic, tears) explosion, to return to Arthur Koestler’s notion of bisociation and its various types and expressions.
But that’s just fun, and will quickly become dated.. that’s an aside.
**
A new category of linkage:
More seriously, I’d like to suggest that one faascinating type of linkage, close kin to “this is similar to that” is the category of mistake:
this is, has been, or can be mistaken for that
My example here is the weird sonic effect that seems to have physically hurt American diplomats and other embassy employees in Cuba, and confused national security analysts —
That headline was taken from an article dated December 12, 2018, less than a month ago at time of writing. Doctors called in to examine embassy workers were flummoxed:
The patients complained of intense ear pain, hearing loss, headaches, dizziness and difficulty with balance, as well as increased anxiety and irritability, doctors found, but who or what caused the damage is still unknown.
From The Atlantic:
Various parties argued that the strange noise was the result of a sonic weapon, a microwave attack, or malfunctioning eavesdropping equipment.
And back to ABC:
“The possible sources and the medical findings we have here do not have a quick or easy solution,” said Dr. Carey Balaban, a professor of otolaryngology at the University of Pittsburgh School of Medicine who contributed to the study. “I wish someone could tell us that right now. I wish we’d have that.”
Damn commie Cubans!
The thing is, otolaryngologists and high-tech security experts were the wrong people to solve the problem. Whenentomologists listened to a recording of the sound, they recognizedd it —
as the mating call of Anurogryllus celerinictus, the Indies short-tailed cricket.
the cricket’s call has been mistaken for a devious commie attack on American diplomats
**
Very briefly, then, to wrap up, since the idea is to link one concept to another, I use graphs as my game boards, assigning the concepts (images, quotes, clips &c) to numbered positions (nodes) on the boards, with the lines between them (edges) representing their associative links, which can be spelled out in however much detail a given game requires:.
top left, the standard WaterBird board; top right, a board from the Sembl game as played on iPads in the National Museum of Australia; lower left, the Doublequote board, for direct comparison of two concepts / images; lower right, the Said Symphony board, for us in “aymphonic” games.
The idea of conceptual graphs precedes Margaret Masterman by centuries:
Left, the Sephirotic Tree of classical Kabbalah; middle: Oronce Fine’s diagram of the elements and humors; right: a medieval Trinitarian diagram
And as a grace note — my two now ancient pages on Masterman, Boole and that Trinitarian diagram are still a quiet delight for scholars of conceptual graphs and the like. Masterman really was an unsung genius, and her curious and vastlky erudite paper Theism as a Scientific Hypothesis proves it..
I wonder when AlphaZero will be playing a game like this: