[ by Charles Cameron — via Christopher Alexander, Arthur Koestler, James Clerk Maxwell, Hermann Hesse, and Wells Cathedral ]
.
My topic today is a comment that John Robb just posted on his FaceBook page. As so often, I’ll proceed by indirection. Here’s a wild DoubleQuote illustrating a blogger’s perceived similarity between the “scissors arch” at Wells Cathedral and one of the models in Jean Paul Gaultier‘s 2009 Spring collection:

**
John Robb posted:
Some philosophical thinking:
Human knowledge, at an elemental level, can be described as a “transformation” of data.
Complex ideas are built using layers of “transformations” with each layer feeding into the next (think pyramid)
We teach these transformations at home and at school to our children.
We communicate by sharing transformations.
Questions We Need to Answer in the Age of Cognitive Machines:
How many transformations would it take to model all human knowledge?
How deep (how many layers of transformation is human knowledge) is human knowledge? Both on average or at its deepest point?
How broad is human knowledge (non-dependent transformations)?
How fast is the number of transformations increasing and how fast is it propagating across the human network?
**
My interest is in John’s pyramid, considered as a pyramid of arches.
My starting point (with Hermann Hesse‘s Glass Bead Game ever in background) is Arthur Koestler‘s observation in The Act of Creation that the creative spark occurs at the intersection of two planes of thought —
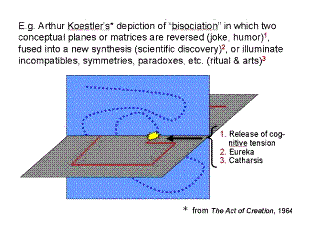
— or to put that another way, that the creative leap is an associative leap between two concepts, disciplines or aspects of knowledge — thus, an arch:
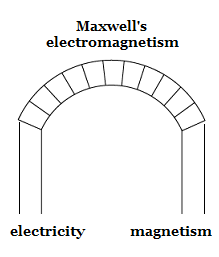
Likewise:
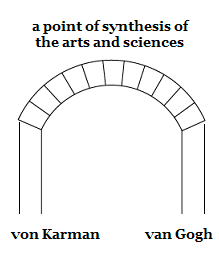
— which in my own DoubleQuotes notation gives us:
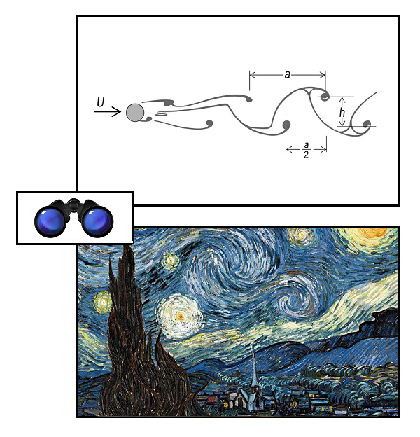
— thus, many arches build to a pyramid:
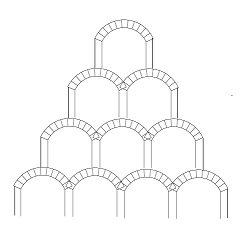
**
Of course, with arches one has to be very circumspect, buecause in rich contexts, they’re not simple creatures:

Among the greatest such arches I know are Taniyama‘s 1955 “surmise” as Barry Mazur puts it, that “every elliptic equation is associated with a modular form” — arching way above my pay grade — an insight that was to bear rich fruit forty years later, in Andrew Wiles‘ proof of Fermat’s Last Theorem; and Erwin Panofsky‘s great book similarly linking the structures of medieval cathedrals and scholastic thought:

**
White we’re on the topic of gothic iconography, another form of arch we might consider is the vesica piscis:
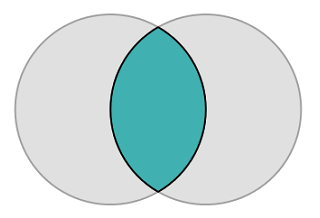
— frequently found in medieval art and architecture:

**
I’m not suggesting, John, that your inquiry and mine are identical — far from it — but that they have a sufficiently rich overlap that an appreciation of one is likely to spark insight in terms of the other.
And with Hesse’s Game, with which I recall from our earlieest conversations you are familiar..
I mentioned Hesse and Christopher Alexander in my bracketed note at the top of this post. It’s my impression that both were striving for a similar encyclopedic architecture to the pyramid John proposes. Hesse on the Glass Bead Game:
All the insights, noble thoughts, and works of art that the human race has produced in its creative eras, all that subsequent periods of scholarly study have reduced to concepts and converted into intellectual values the Glass Bead Game player plays like the organist on an organ. And this organ has attained an almost unimaginable perfection; its manuals and pedals range over the entire intellectual cosmos; its stops are almost beyond number. Theoretically this instrument is capable of reproducing in the Game the entire intellectual content of the universe.
And Hesse is clear that individual moves within the games take the form of parallelisms, resemblances, analogical leaps — writing, for instance:
Beginners learned how to establish parallels, by means of the Game’s symbols, between a piece of classical music and the formula for some law of nature.
Speaking of the playing of his great Game, Hesse said:
I see wise men and poets and scholars and artists harmoniously building the hundred-gated cathedral of the mind.
And Alexander? His book A Pattern Language is pretty clearly his own variant on a Glass Bead Game, following on from what he terms his Bead Game Conjecture (1968 – p. 75 at link):
That it is possible to invent a unifying concept of structure within which all the various concepts of structure now current in different fields of art and science, can be seen from a single point of view. This conjecture is not new. In one form or another people have been wondering about it, as long as they have been wondering about structure itself; but in our world, confused and fragmented by specialisation, the conjecture takes on special significance. If our grasp of the world is to remain coherent, we need a bead game; and it is therefore vital for us to ask ourselves whether or not a bead game can be invented.
**
Gentle readers:
For your consideration, delight, temptation, confusion or disagreement, here are three more of Gaultier’s arches, as perceived by Kayan’s Design World:



















